Definicja

Macierz odwrotna do $A$ to macierz $A^{-1}$, która spełnia następującą zależność.

$$AA^{-1} = A^{-1}A = [1]$$

Oznacza to, że macierz $A$, razy jej odwrotność jest tym samym co jej odwrotność razy $A$, czyli macierz jednostkowa, którą oznaczyliśmy tutaj $[1]$. Mnożenie macierzy generalnie nie jest przemienne, ale w tym przypadku nie ma znaczenia, z której strony przemnożymy oryginalną macierz przez jej odwrotność. Wynik będzie taki sam.

Warunki istnienia macierzy odwrotnej?

Kiedy istnieje macierz odwrotna? Nie każda macierz posiada odwrotność. Oby ona istniała, należy spełnić dwa warunki.

1. macierz A jest kwadratowa
2. wyznacznik A jest różny od zera

Jeśli powyższe warunki są spełnione to mówimy, że $A$ jest odwracalna, a jeśli przynajmniej jeden z nich nie jest spełniony to jest ona nieodwracalna.

Wzór na macierz odwrotną

Pierwszą metodą liczenia odwrotności jest skorzystanie ze wzoru na odwrotność.

$$A^{-1} = (A^D)^T * \frac{1}{|A|}$$

Objaśnienie symboli:

• $A^{-1}$ : Macierz odwrotna
• $A^D$ : Macierz dopełnień algebraicznych (w dalszej części nauczymy się ją obliczać)
• $(...)^T$ : Transpozycja
• $\frac{1}{|A|}$ : Odwrotność wyznacznika

Macierz dopełnień algebraicznych $A^D$

Dosyć niejasnym elementem może być macierz dopełnień algebraicznych, dlatego zajmiemy się wyjaśnieniem.

Macierzą dopełnień algebraicznych, czyli $A^D$ będzie macierz utworzona z dopełnień algebraicznych elementów na konkretnych pozycjach z odpowiednim znakiem.

$$A^D=\begin{bmatrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{bmatrix}$$

Jak tworzy się takie dopełnienia?

Przykładowo, $A_{11}$ powstaje poprzez wykreślenie pierwszego wiersza i pierwszej kolumny macierzy $A$. Jest to po prostu wyznacznik z macierzy ułożonej z niewykreślonych elementów przemnożony przez -1 podniesione do potęgi będącej sumą indeksu wykreślanego wiersza (1) oraz kolumny (1). Pierwszy wiersz (1) dodać pierwsza kolumna (1) daje 2, a więc parzystą potęgę, która kasuje minus.

$$A_{11} = \begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix} * (-1)^{1 + 1}$$

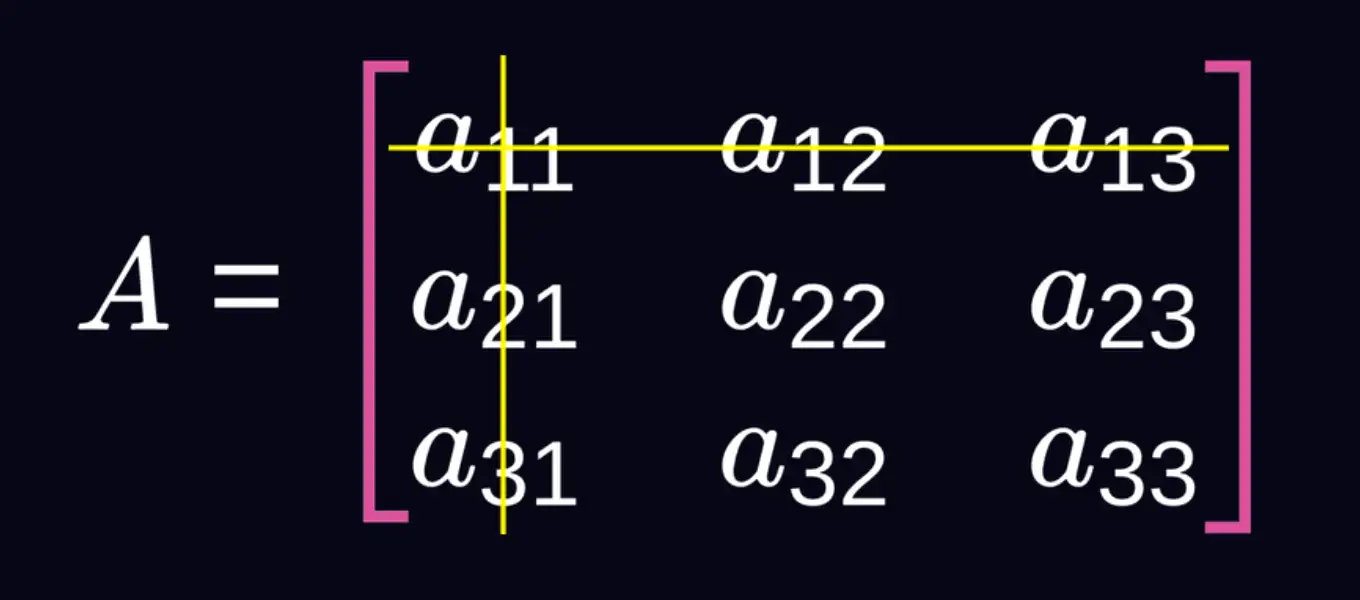
$A_{12}$ powstaje jako wykreślenie pierwszego wiersza i drugiej kolumny. Tym razem suma numeru wiersza i kolumny jest nieparzysta, więc musimy odwrócić znak obliczonego wyznacznika. Minus jeden do nieparzystej potęgi to wciąż minus jeden.

$$A_{12} = \begin{vmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{vmatrix} * (-1)^{1 + 2}$$

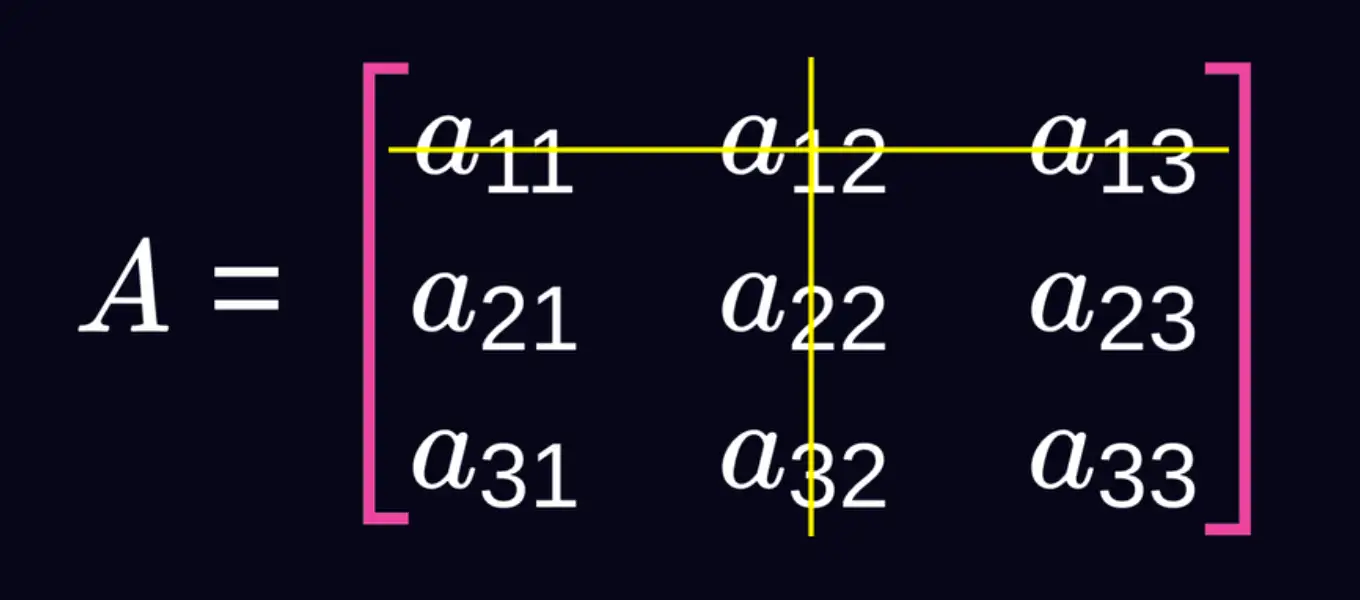
$A_{13}$ powstaje poprzez wykreślenie pierwszego wiersza i trzeciej kolumny. Tym razem potęga przy -1 jest parzysta, co daje zwykłe mnożenie przez 1.

$$A_{12} = \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \end{vmatrix} * (-1)^{1 + 3}$$

Postępujemy analogicznie dla wszystkich elementów macierzy $A$. Wychodzi na to, że macierz dopełnień to po prostu macierz złożona z wyznaczników (czyli liczb), które mnożymy przez -1 gdy suma indeksu wiersza i kolumny jest nieparzysta. Gdy suma indeksów jest parzysta to mnożymy przez 1, czyli w zasadzie nic nie robimy 😉.

Gotowa macierz dopełnień algebraicznych dla przykładu 3x3 wygląda tak jak poniżej. Trochę strasznie, ale pamiętaj, że wyznaczniki to po prostu liczby, więc jak już je obliczymy, to ta macierz będzie WIZUALNIE mniejsza.

Tutaj elementami macierzy są wyznaczniki 2x2, które obliczymy na krzyż. Jednak gdyby w środku znajdowały się macierze 3x3 to skorzystamy z reguły Sarrusa a dla większych niż 3x3 z rozwinięcia Laplace'a.

Przykład na konkretnych liczbach

Teraz to na co pewnie czekałeś, czyli przykład odwracania macierzy obliczony nie na symbolach a konkretnych liczbach.

Oczywiście skorzystamy właśnie ze wzoru, który przed chwilą został objaśniony.

Zajmiemy się taką macierzą A. Macierze-i-wektory/pl/chapter-05/lesson-02/notes/macierzA.png

Krok 1: obliczenie wyznacznika

$A^{-1}=(A^D)^T * \frac{1}{\color{blue}|A|}$

Odwracanie macierzy dowolną metodą zaczynamy zawsze od sprawdzenia, czy jest ona w ogóle odwracalna, czyli obliczamy wyznacznik i sprawdzamy, czy jest on różny od 0, ponieważ we wzorze $A^{-1}=(A^D)^T * \frac{1}{|A|}$ dzielimy przez $|A|$, więc musimy uniknąć dzielenia przez 0.

A jest macierzą 3x3, więc idealnie spisze się tutaj metoda Sarrusa, gdzie dopisujemy na dole dwa pierwsze wiersze i sumujemy iloczyny na przekątnych i następnie odejmujemy zsumowane iloczyny na przeciwprzekątnych.

Dobrze się składa, bo $|A|=-15$ a więc istnieje odwrotność.

Krok 2: obliczenie macierzy dopełnień algebraicznych

$A^{-1}=(\textcolor{blue}{A^D})^T * \frac{1}{|A|}$

Jak już mamy wyznacznik to musimy zająć się obliczeniem macierzy dopełnień algebraicznych. To jest najbardziej czasochłonny krok całego odwracania macierzy.
Wiemy, że $A^D$ będzie macierzą 3x3, czyli takiego samego wymiaru jak $A$, ale będzie się składała z wyznaczników. Wygodnie będzie od razu wpisać sobie do $A^D$ dziewięć takich jeszcze nieobliczonych wyznaczników.
Już na tym etapie możemy wpisać minusy przed odpowiednimi wyznacznikami. Zapamiętaj tylko, że lewy górny róg ma znak dodatni a reszta znaków idzie na zmianę minus i plus.

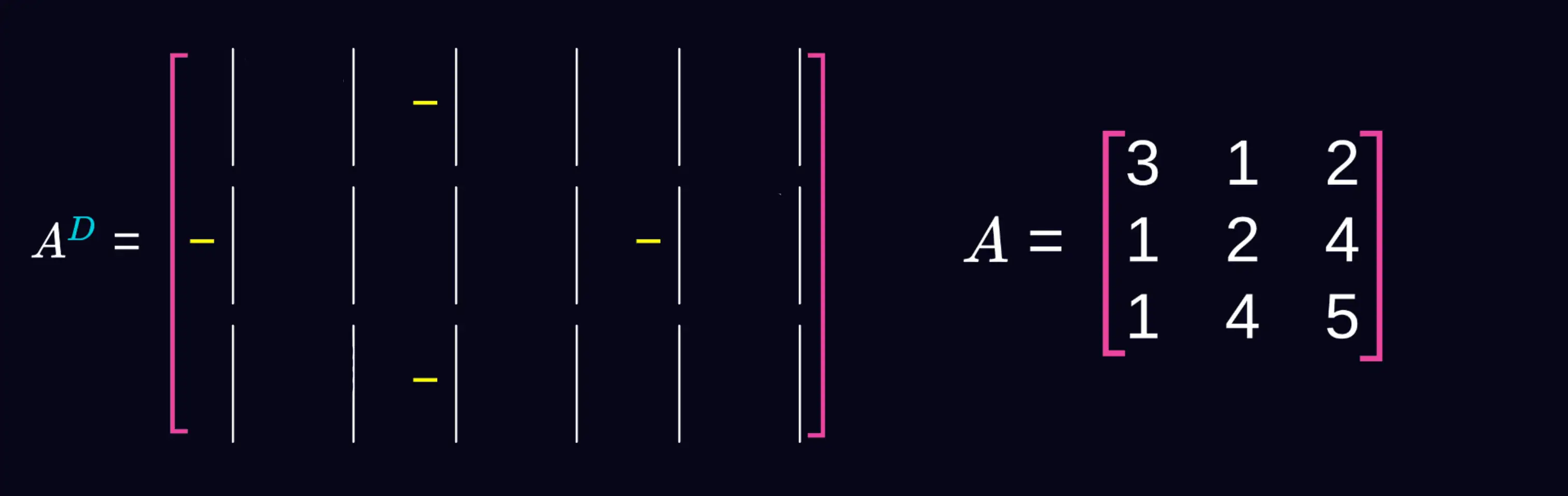
Wykreślamy pierwszy wiersz i pierwszą kolumnę i w tym samym miejscu w nowej macierzy tworzymy wyznacznik z niewykreślonych elementów macierzy A

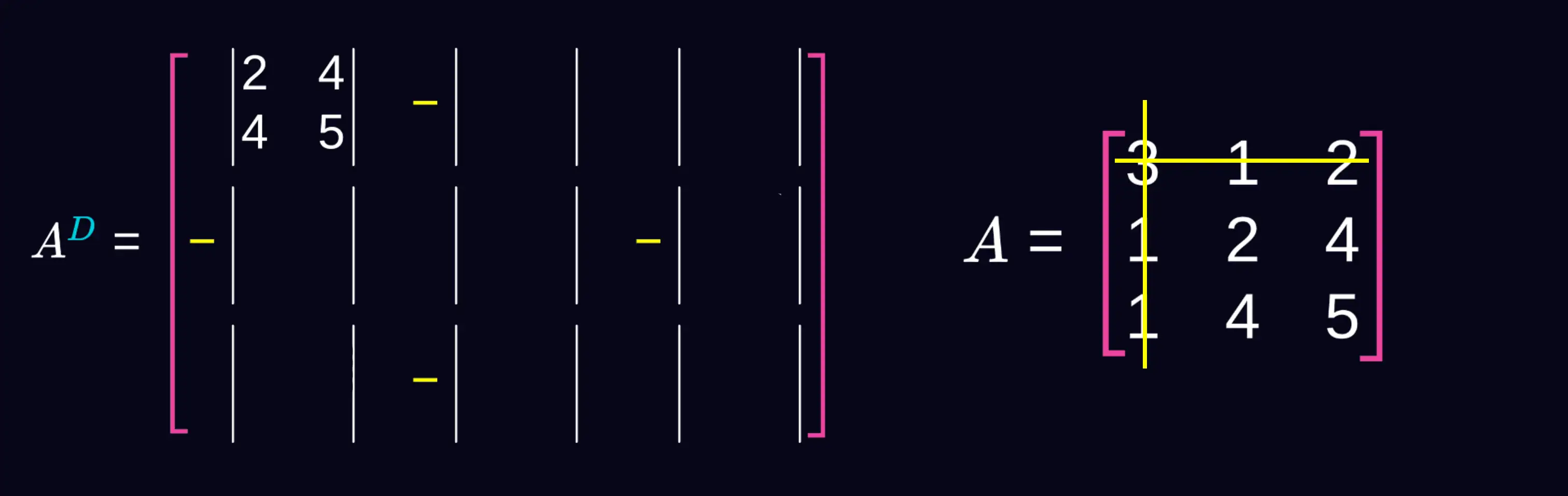
Następnie wykreślamy pierwszy wiersz i drugą kolumnę

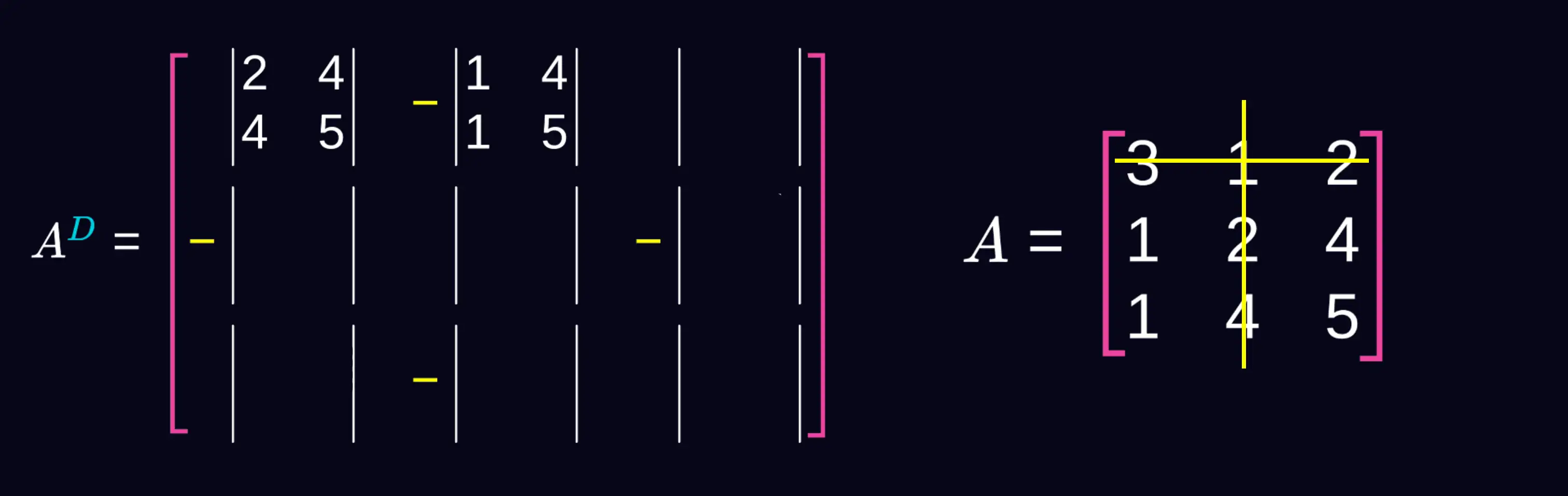
Pierwszy wiersz i trzecią kolumnę

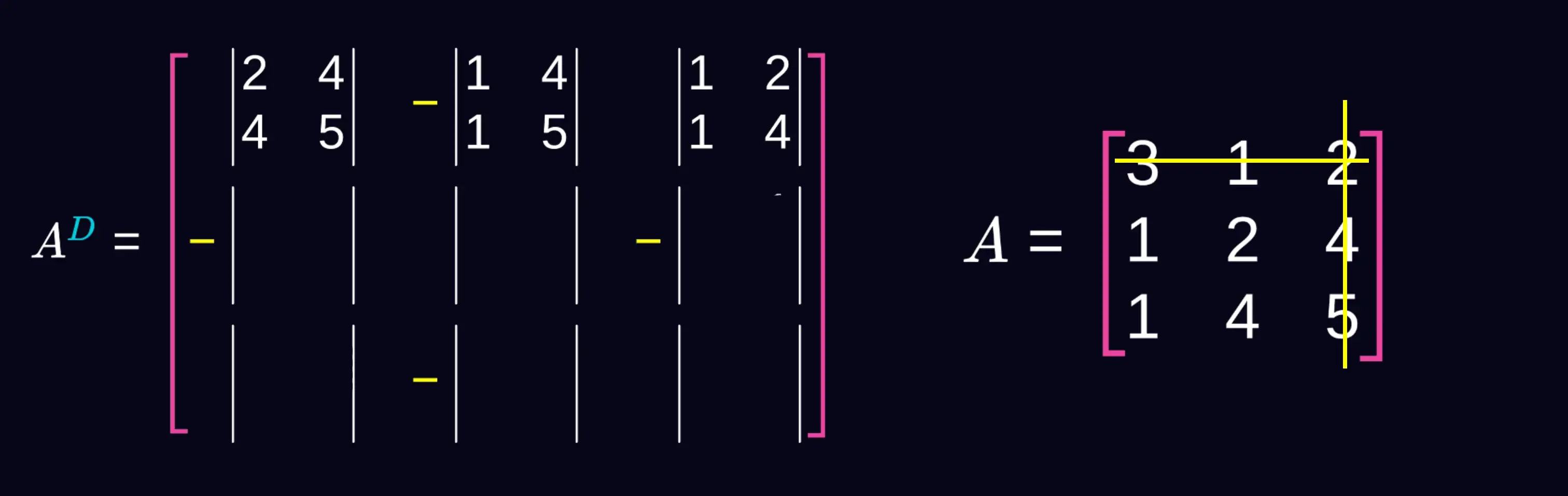
Drugi wiersz i pierwszą kolumnę

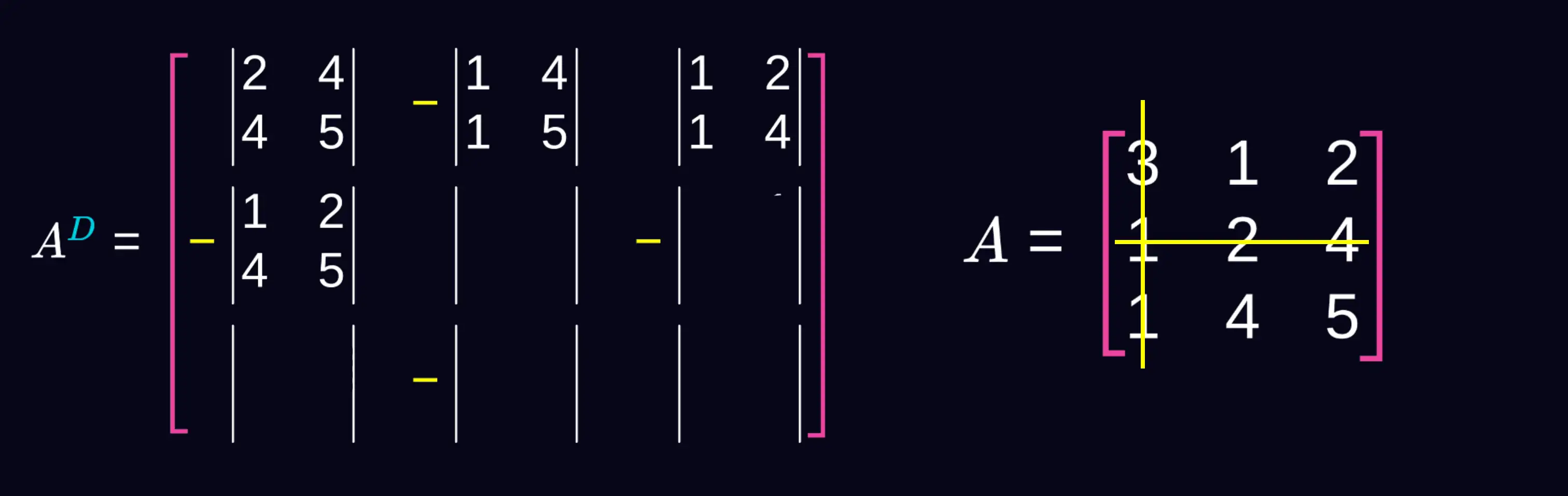
Drugi wiersz i druga kolumnę

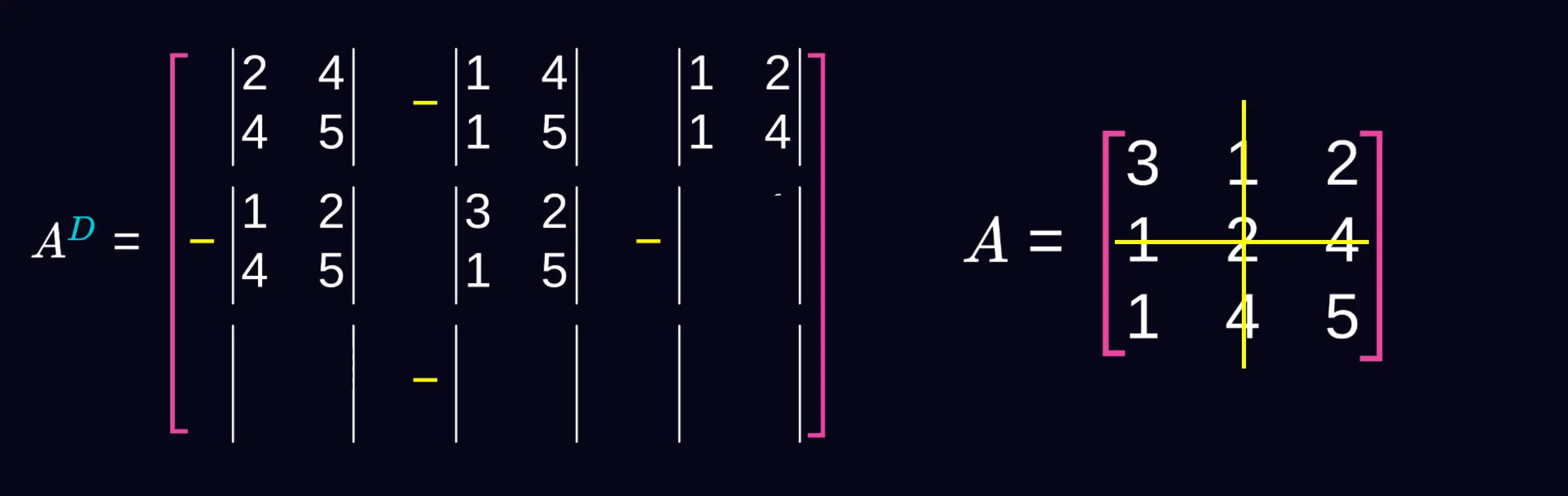
Drugi wiersz i trzecią kolumnę

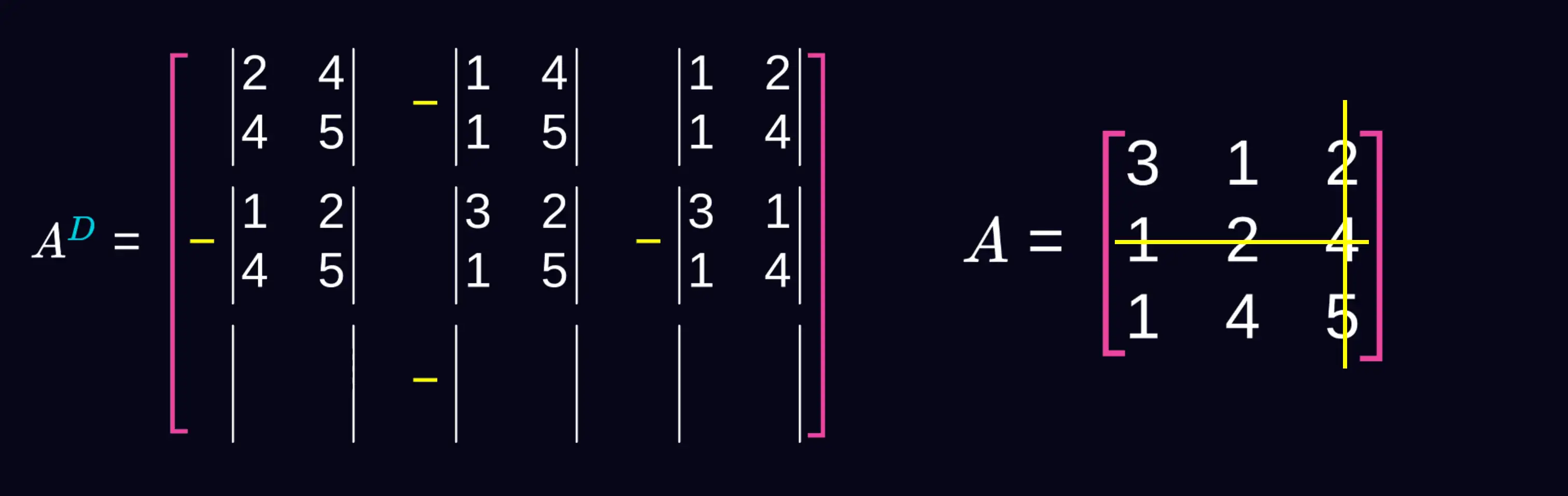
Trzeci wiersz i pierwszą kolumnę

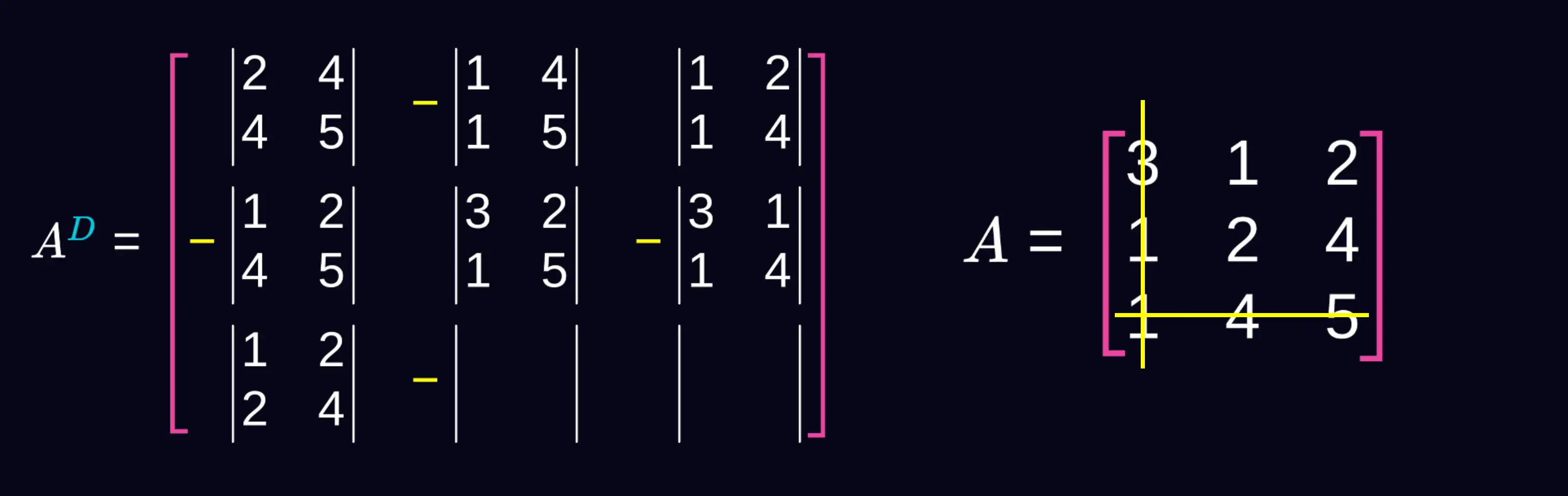
Trzeci wiersz i drugą kolumnę

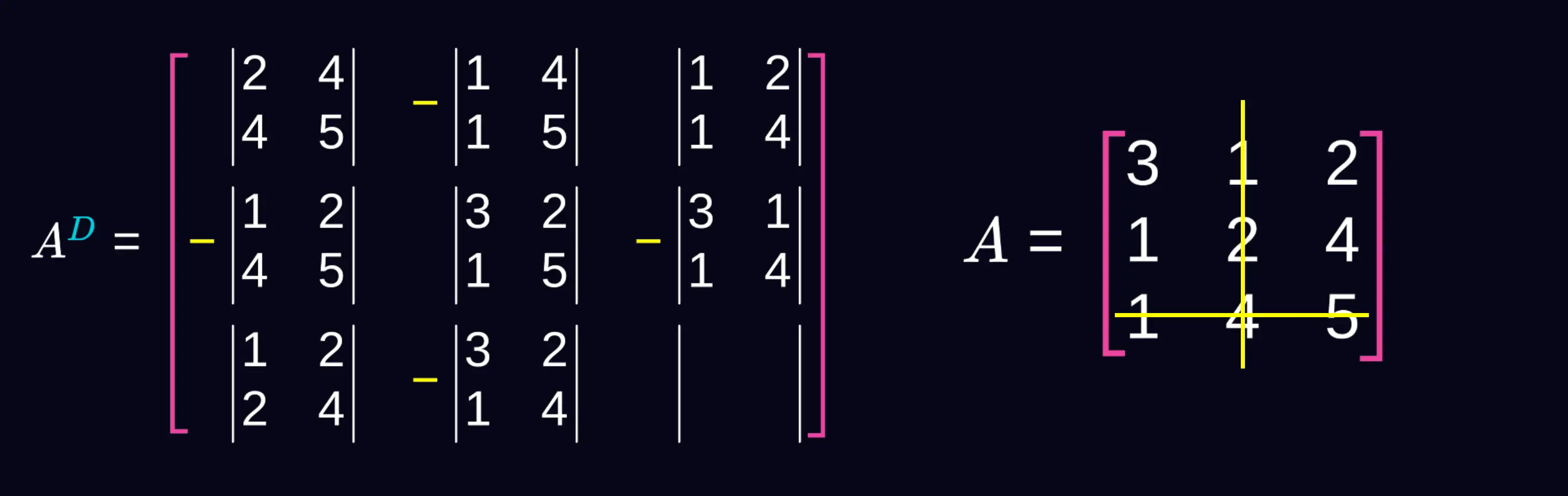
Trzeci wiersz i trzecią kolumnę. To już jest macierz dopełnień algebraicznych.

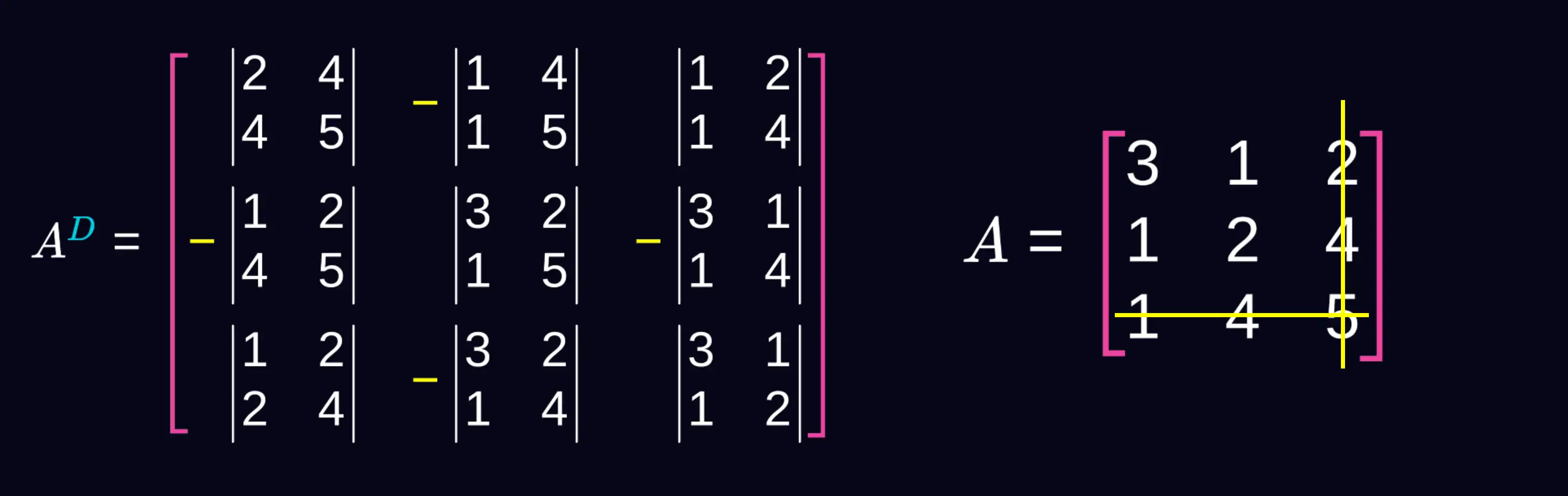
Pozostaje nam jeszcze obliczyć wszystkie wyznaczniki i uwzględnić minusy w wynikach.

$$A_{11}=2 * 5 - 4 * 4 = 10 - 16 = -6 \\ A_{12}=-(1 * 5 - 1 * 4) = -1 \\ A_{13}=1 * 4 - 2 * 1 = 2 \\ A_{21}=-(1 * 5 - 2 * 4) = 3 \\ A_{22}=3 * 5 - 2 * 1 = 13 \\ A_{23}=-(3 * 4 - 1 * 1) = -11 \\ A_{31}=1 * 4 - 2 * 2 = 0 \\ A_{32}=-(3 * 4 - 2 * 1) = -10 \\ A_{33}=3 * 2 - 1 * 1 = 5 \\$$

Wpisujemy wszystkie wyniki do macierzy i oto gotowa macierz dopełnień algebraicznych.

$$A^D=\begin{bmatrix} -6 & -1 & \phantom{-}2 \\ \phantom{-}3 & \phantom{-}13 & -11 \\ \phantom{-}0 & -10 & \phantom{-}5\end{bmatrix}$$

Krok 3: transpozycja macierzy dopełnień algebraicznych

$A^{-1}={\color{blue}(A^D)^T} * \frac{1}{|A|}$

Jedyne co musimy zrobić na tym etapie to przetransponować $A^D$ otrzymaną w poprzednim kroku. Zamieniamy miejscami kolumny z wierszami.

$(A^D)^T= \begin{bmatrix} -6 & -1 & \phantom{-}2 \\ \phantom{-}3 & \phantom{-}13 & -11 \\ \phantom{-}0 & -10 & \phantom{-}5\end{bmatrix}^T=$ $\begin{bmatrix} -6 & \phantom{-}3 & \phantom{-}0\\ -1 & \phantom{-}13 & -10\\ \phantom{-}2 & -11 & \phantom{-}5 \end{bmatrix}$

Krok 4: przemnożenie przez odwrotność wyznacznika

$A^{-1}=(A^D)^T * {\color{blue} \frac{1}{|A|}}$

Ostatni etap odwracania macierzy sprowadza się po prostu do przemnożenia każdego elementu transponowanej macierzy otrzymanej w poprzednim kroku przez odwrotność wyznacznika. Nam wyszło, że $|A|=-15$, więc mnożymy wszystko przez $-\frac{1}{15}$. Macierz w żółtej ramce to gotowa macierz odwrotna, czyli $A^{-1}$

$(A^D)^T * \frac{1}{|A|}=\begin{bmatrix} -6 & \phantom{-}3 & \phantom{-}0\\[3pt] -1 & \phantom{-}13 & -10\\[3pt] \phantom{-}2 & -11 & \phantom{-}5\end{bmatrix}* \frac{1}{-15}$ $= \begin{bmatrix} \phantom{-} \frac{2}{5} & -\frac{1}{5} & \phantom{-} 0 \\[3pt] \phantom{-} \frac{1}{15} & -\frac{13}{15} & \phantom{-} \frac{2}{3} \\[3pt] -\frac{2}{15} & \phantom{-} \frac{11}{15} & -\frac{1}{3}\end{bmatrix}$