✏️ Rzuty:

W tym artykule udostępniliśmy fragment lekcji dotyczący równi pochyłej, z kursu Dynamika. Omówiono w niej dokładnie sytuację, w której pojedyńcze ciało znajduje się na równi pochyłej, krok po kroku przeanalizowano jakich sił doznaje masa, a także wyprowadzono wszystkie niezbędne wzory. Uwaga! Omawiany przypadek dotyczy ruchu bez oporów!

Definicja

Rzut to pojęcie stosowane w fizyce do opisu ruchu ciała w pole grawitacyjnym, który intuicyjnie wyobrażamy jako spadek lub wznoszenie przy określonych parametrach. Na ogół rozróżniamy trzy rodzaje rzutów:

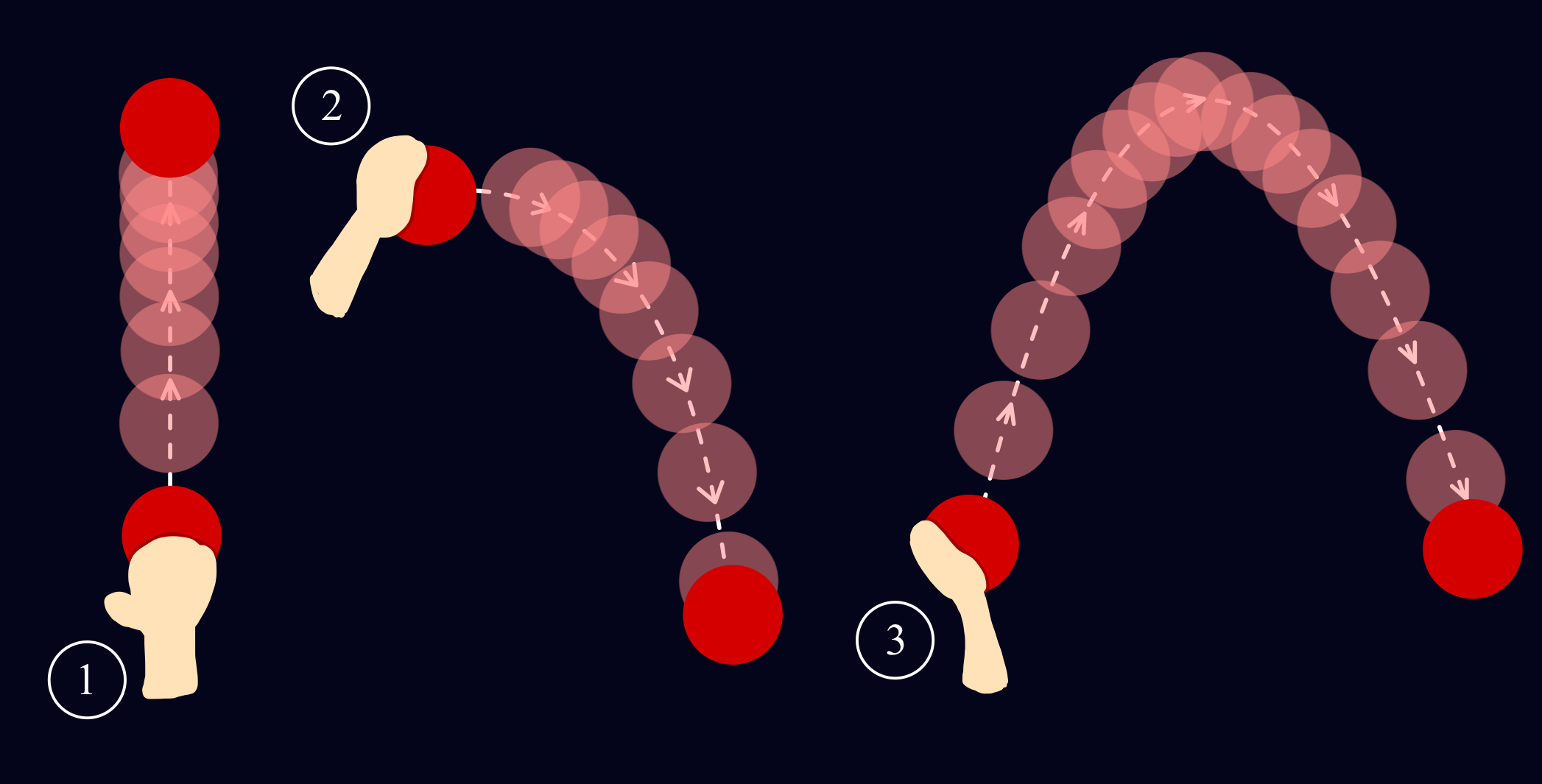
1. Rzut pionowy - to wyrzucenie ciała pionowo do góry, czyli nadanie ciału prędkości początkowej $v_0$, skierowanej w górę. Na poniższym rysunku możesz zobaczyć jak schematycznie wygląda taki ruch.
2. Rzut poziomy - to wyrzucenie ciała poziomo w bok, prawo, lub lewo. W takim wypadku nadajemy ciału prędkość początkową $v_0$ tylko względem osi X. Spójrz na rysunek nr 2, żeby zorientować się jak to wygląda z boku.
3. Rzut ukośny - to wyrzucenie ciała pod pewnym kątem $\beta$ do góry, czyli nadanie pewnej prędkości ciału zarówno w pionie, jak i w poziomie. Na trzecim rysunku pokazano przykładowych schamat takiego rzutu.
   

Wzory

Żeby móc w pełni opisać i przewidzieć to, jak zachowuje się ciało podczas dowolnego, z wymienionych rzutów, musimy wykorzystujemy określone parametry:

• Funkcja położenia $x(t),\;y(t)$ - w zależności od rodzaju rzutu, może składać się z funkcji opisującej położenie ciała w czasie względem osi X i Y;
• Funkcja opisująca prędkość ciała $v_x(t),\;v_y(t)$ - podobnie jak położenie, może być niezerowa względem osi X i Y;
• Przyspieszenie ciała $a$ - w podręcznikowym rzucie poziomym ciało znajduje się w polu grawitacyjnym, a więc jedynym przyspieszeniem, jakiego to ciało doznaje jest przyspieszenie ziemskie $g$, które jest skierowane pionowo w dół;
• Ekstremalne wartości - takie jak maksymalna wysokość osiągana przez ciało $h_{max}$, $y_{max}$, czy też zasięg rzutu $x_u$, $x_{max}$, czyli miejsce względem osi X w którym upada ciało.
• Całkowity czas trwania ruchu $t_c$;
• Funkcja toru ciała $y(t)$ - funkcja, w które położenie pionowe piłki jest uzależnione od jej położenia poziomego. Znajdując, lub wykreślając taką funkcję - możemy bez problemu zobaczyć, a dzięki temu - zbadać jak wygląda ruch. Poniżej przedstawiono rozbudowane tabelki ze wzorami, które opisują te parametry maetmatycznie dla różnych rodzajów rzutów.

Rzut poziomy

wersja do pobrania

Rzut pionowy

wersja do pobrania

Rzut ukośny

wersja do pobrania

Przykład 1

Ciało wyrzucono pionowo z prędkością $v_0=6\;\frac{\text{m}}{\text{s}}$. a) Ile czasu trwał ruch ciała? b) Jaką maksymalną wysokość osiągnie ciało?

Rozwiązanie Podpunkt a): Zaczynamy od wykorzystania wzoru na czas, który zajął ciału osiągnąć wysokość maksymalną (z tabelki ze wzorami): $t_{max} = \frac{v_0}{g}=\frac{1}{2}t_c$ Potrzebujemy tylko jego drugiej części, czyli wyrażenia po pierwszym i drugim znaku równości: $\frac{v_0}{g}=\frac{1}{2}t_c$ Tak jak $t_c$ to oznaczenie na czas trwania całego ruchu, musimy tak przekształcić wyrażenie, by obliczyć go. W tym celu mnożeymy równanie obustronnie przez 2: $\frac{v_0}{g}=\frac{1}{2}t_c\quad|\cdot2\quad$ $t_c=\frac{2v_0}{g}$ Pozostaje tylko podstawić liczby i obliczyć wynik: $t_c=\frac{2\cdot6\;\frac{\text{m}}{\text{s}}}{9.8\;\frac{\text{m}}{\text{s}^2}}\approx1.2\text{ s}$

Odpowiedż: $t_c=1.2\text{ s}$.

Podpunkt b): By obliczyć maksymalną wysokość nie musimy kombinować, po prostu wykorzystamy wzór na maksymalną wysokość, jaką osiągnie ciało: $h_{max}=\frac{v_0^2}{2g}+y_0$ Przy czym w tym zadaniu - możemy bez problemu uznać, że $y_0$ jest równe zero: $h_{max}=\frac{v_0^2}{2g}$

Podstawiamy dane: $h_{max}=\frac{(6\;\frac{\text{m}}{\text{s}})^2}{2\cdot 9.8\;\frac{\text{m}}{\text{s}^2}}\approx1.8\text{ m}$

Odpowiedż: $h_{max}=1.8\text{ m}$.

Zadanie 1

Z jaką prędkością należy wyrzucić ciało pionowo, by osiągnęło ono wysokość 3 metrów?

Odpowiedż: $v=7.7\;\frac{\text{m}}{\text{s}}$.

Zadanie 2

W której sekundzie ruchu ciało, wyrzucone z prędkością $v_0=12\;\frac{\text{m}}{\text{s}}$, osiągnie wysokość 1.5 m?

Odpowiedź: $t_1=0.13\text{ s}$ i $t_2=2.32\text{ s}$.

Przykład 2

Ciało wyrzucono poziomo z wysokości $5\text{ m}$. Wiadomo, że upadło ono w odległości $x_u=12\text{ m}$ od miejsca wyrzucenia. Oblicz: a) Z jaką prędkością wyrzucono ciało; b) Ile czasu trwał ruch ciała; c) Z jaką prędkością ciało wylądowało.

Rozwiązanie Podpunkt a): Tak jak w zadaniu podano dokładne dane dotyczące wysokości z jakiej wyrzucono ciało $y_0$, a także zasięgu $x_u$, możemy śmiało skorzystać ze wzoru zasięg rzutu ciała (z tabelki): $x_u=v_0\sqrt{\frac{2y_0}{g}}+x_0$ W tym zadaniu możemy śmiało uznać, że $x_0$, czyli położenie początkowe ciała względem osi X jest równe zeru: Tak jak w zadaniu podano dokładne dane dotyczące wysokości z jakiej wyrzucono ciało $y_0$, a także zasięgu $x_u$, możemy śmiało skorzystać ze wzoru zasięg rzutu ciała (z tabelki): $x_u=v_0\sqrt{\frac{2y_0}{g}}$ Należy jedynie przekształcić równanie tak, by wyznaczyć z niego $v_0$. Dzielimy więc wszystko na pierwiastek: $x_u=v_0\sqrt{\frac{2y_0}{g}}\quad |:\sqrt{\frac{2y_0}{g}}$ $v_0=x_u\sqrt{\frac{g}{2y_0}}$ Pozostaje tylko podstawić dane: $v_0=12\text{ m}\cdot\sqrt{\frac{9.8\;\frac{\text{m}}{\text{s}^2}}{2\cdot 5\text{ m}}}\approx11.9\;\frac{\text{m}}{\text{s}}$

Odpowiedź: $v_0=11.9\;\frac{\text{m}}{\text{s}}$.

Podpunkt b): Obliczyć czas trwania ruchu możemy na kilka sposobów. Tak jak znamy już prędkość, a zasięg jest podany w treści - możemy skorzystać z funkcji na położenie ciała względem osi X, podstawiając do niego za argument całkowity czas trwania ruchu: $x(t_c)=x_u=v_0t_c+x_0$ Ale możemy również wykorzystać gotowy wzór na czas upadku ciała (z tabelki): $t_{c} = \sqrt{\frac{2y_0}{g}}$ Do drugiego wzoru wystarczy podstawić dane i można obliczyć wynik, więc najłatwiej jest wykorzystać ten sposób: $t_{c} = \sqrt{\frac{2\cdot 5\text{ m}}{9.8\;\frac{\text{m}}{\text{s}^2}}}\approx1.01\text{ s}$

Odpowiedź: $t_c=1.01\text{ s}$.

Podpunkt c): By obliczyć prędkość, jaką osiągnęło ciało, gdy wylądowało - możemy wykorzystać wozory na funkcje prędkości ciała: $\vec{v}=[v_0,-gt]$ Należy tylko podstawić odpowiednią wartość czasu $t$. Będzie to oczywiście $t_c$, chwila, kiedy ruch ciała się zakończył: $\vec{v}=[v_0,-gt_c]$ A tak jak wszystkie dane mamy podane w treści, możemy je podstawić do wzoru: $\vec{v}=\left[11.9\;\frac{\text{m}}{\text{s}},-9.8\;\frac{\text{m}}{\text{s}^2}\cdot 1.01\text{ s}\right]=\left[11.9\;\frac{\text{m}}{\text{s}},-9.9\;\frac{\text{m}}{\text{s}}\right]$ Mamy jednak narazie tylko współrzędne wektora prędkości. Obliczamy jeszcze tylko jego wartość: $|\vec{v}|=\sqrt{\left(11.9\;\frac{\text{m}}{\text{s}}\right)^2+\left(-9.9\;\frac{\text{m}}{\text{s}}\right)^2}=15.5\;\frac{\text{m}}{\text{s}}$

Odpowiedź: $|\vec{v}_k|=15.5\;\frac{\text{m}}{\text{s}}$.

Zadanie 3

Ciało wyrzucono poziomo z prędkością $v_0=7\;\frac{\text{m}}{\text{s}}$, a upadło ono 14 m od punktu wyrzucenia. Oblicz: a) Wysokość z jakiej ciało upadło; b) W której sekundzie ruchu ciało miało prędkość v=8;\frac{\text{m}}{\text{s}}; c) Wysokość, na jakiej ciało się znadowało wtedy.

Odpowiedż: a) $y_0=19.6\text{ m}$, b) $t=0.4\text{ s}$, c) $h=18.8\text{ m}$.

Zadanie 4

Ruch ciała, które wyrzucono poziomo trwał 2.5 sekundy. Zasięg rzutu był trzy razy większy od wysokości, z jakiej to ciało wyrzucono. Oblicz prędkość początkową $v_0$.

Odpowiedż: $v_0=36.8\;\frac{\text{m}}{\text{s}}$.

Przykład 3

Pod kątem $20^\circ$ chłopiec wyrzucił przed siebie kamień i trafił w ptaka, który siedział na drzewie, 12 metrów przed nim. Wiedząc, że wysokość, na jakiej siedział kruk to 4 metry, oblicz z jaką prędkością wyrzucono kamień.

Rozwiązanie

By znaleźć prędkość wyrzucenia ciała, najlepiej będzie wykorzystać wzory na funkcje położeń ciała wezględem obu współrzędnych: $[x(t),y(t)]=[|\vec{v}|\cdot t\cos(\beta)+x_0,|\vec{v}|\cdot t\sin(\beta)-\frac{1}{2}gt^2+y_0]$

Przy czym - najlepiej zapisać je jako układ równań: $\begin{cases} x(t)=|\vec{v}|\cdot t\cos(\beta)+x_0\\ y(t)=|\vec{v}|\cdot t\sin(\beta)-\frac{1}{2}gt^2+y_0 \end{cases}$

Przy czym za wartości $x(t)$ i $y(t)$ podstawmy punkt, w którym znajduje się ptak, w którego trafiono. Oznaczymy go narazie jako $x_1$ i $y_1$: $\begin{cases} x_1=|\vec{v}|\cdot t\cos(\beta)+x_0\\ y_1=|\vec{v}|\cdot t\sin(\beta)-\frac{1}{2}gt^2+y_0 \end{cases}$

Ponadto - możemy uznać, że punkt początkowy $(x_0,y_0)$ jest początkiem układu współrzędnych, a więc $x_0$ i $y_0$ są po prostu zerem: $\begin{cases} x_1=|\vec{v}|\cdot t\cos(\beta)\\ y_1=|\vec{v}|\cdot t\sin(\beta)-\frac{1}{2}gt^2 \end{cases}$

A następnie - pierwsze równanie dzielimy na $|\vec{v}|\cdot\cos(\beta)$, żeby wyznaczyć z niego $t$, a następnie podstawiamy tak wyznaczone wyrażenie do drugiego równania: $\begin{cases} t=\frac{x_1}{|\vec{v}|\cdot \cos(\beta)}\\ y_1=|\vec{v}|\cdot \frac{x_1}{|\vec{v}|\cdot \cos(\beta)}\cdot\sin(\beta)-\frac{1}{2}g\left(\frac{x_1}{|\vec{v}|\cdot \cos(\beta)}\right)^2 \end{cases}$

A dalej będziemy zajmować się tylko drugim równaniem. Upraszamy je najbardziej jak się da, skracając powtarzające się wartości i upraszczając wyrażenia trygonometryczne: $y_1= x_1\cdot\tan(\beta)-\frac{gx_1^2}{2|\vec{v}|^2\cdot \cos^2(\beta)}$

A tak jak mamy znaleźć prędkość, z jaką wyrzucono ciało, przekształcamy je tak, by wyznaczyć z niego $v$. W tym celu przenosimy na prawą stronę wyrażenie z szukaną prędkością na lewą, a wszytsko pozostałe - na prawą: $\frac{gx_1^2}{2|\vec{v}|^2\cdot \cos^2(\beta)}= x_1\cdot\tan(\beta)-y_1$

Teraz mnożymy wszystko na krzyż, dzięki czemu uzyskujemy $v^2$ w liczniku: $2|\vec{v}|^2 \cos^2(\beta)\cdot(x_1\cdot\tan(\beta)-y_1)=gx_1^2$ Pozostaje tylko podzielić obustronnie przez czynnik przy $v$: $|\vec{v}|^2 =\frac{gx_1^2}{2\cos^2(\beta)\cdot(x_1\cdot\tan(\beta)-y_1)}$

I spierwiastkować: $|\vec{v}| =\sqrt{\frac{gx_1^2}{2\cos^2(\beta)\cdot(x_1\cdot\tan(\beta)-y_1)}}$

Pod koniec podstawiamy dane i obliczamy wynik: $|\vec{v}| =\sqrt{\frac{9.8\;\frac{\text{m}}{\text{s}^2}\cdot (12\text{ m})^2}{2\cos^2(20^\circ)\cdot(12\text{ m}\cdot\tan(20^\circ)-4\text{ m})}}\approx 46.6\;\frac{\text{m}}{\text{s}}$

Odpowiedż: $|\vec{v}|=46.6\;\frac{\text{m}}{\text{s}}$.

Zadanie 5

Pod jakim kątem należy wyrzucić ciało, by upadło ono jak najdalej od osoby, która go wyrazuciła?

Odpowiedż: $\alpha=45^\circ$

Zadanie 6

Ile czasu będzie spadała piłka, którą wyrzucono pod kątem $\beta=10^\circ$, a jej zasięg był równy $4\text{ m}$? Z jaką prędkością ją wyrzucono?

Odpowiedż: $t_c=0.38\text{ s}$, $v_0=10.7\;\frac{\text{m}}{\text{s}}$.

Zadanie 7

Kosz do gry w koszykówkę znajduje się na wysokości $h=3\text{ m}$. Zawodnik stoi w odległości 8 metrów od niego, jednak ze względu na dużą liczbę napastników, musi wyrzucić piłkę po kątem $\alpha=80^\circ$. Z jaką prędkością musi to zrobić, by trafić do kosza? Przyjmij, że jego wysokość (cdzyli wysokość, z jakiej wyrzuca piłkę) jest równa $1.95\text{ m}$.

Odpowiedż: $v=15.3\;\frac{\text{m}}{\text{s}}$.